티스토리 뷰
일단 기본 루틴에 대해서 살펴봤었다...
1. centroid를 계산하고(초기는 랜덤 등..)
2. 모든 데이터에 대해서 최소 거리의 centroid로 할당하고
3. 2번에서 더이상 변하는 데이터가 없을 경우 종료
간단하다.. 중요한 것이 centroid를 구하는 것, 최소 거리의 centroid를 구하는 것 정도일 것이다.
또 중요한 점이 있다면 벡터 공간상에서 가능할 것이라는 것, 1d의 스칼라 값 뿐만 아니라 2d의 벡터 값에서도 클러스터링을 지원해줄 수 있도록 좀 범용적으로 활용할 수 있도록 하면 좋을 것이다.
따라서, 초기 입력을 float*의 데이터를 받고, 클래스 내부에서는 vector<float>형으로 다루기로 하자.
필요한 변수는
k개의 클러스터 : m_nK
centroid의 정보 : vector<vector<float>> m_vecCentroids
데이터가 분류된 cluster의 정보 : vector<int> m_vecCluster
data정보 : vector<vector<float>> m_vecData
centroid의 정보 : vector<vector<float>> m_vecCentroids
데이터가 분류된 cluster의 정보 : vector<int> m_vecCluster
data정보 : vector<vector<float>> m_vecData
필요한 함수는
0. 데이터를 설정하는 함수
1. KMeansClustering을 실행하는 함수(iterate함수)
2. centroid를 계산하는 함수
3. centroid에 대하여 data를 재배치 하는 함수
그래서 0 번 호출-> 1번 호출하면..
1번에서는
1. centroid를 적당하게 init을 해주고
2. data를 재배치(3번 함수)해서 재배치가 없다면 결과 리턴
3. 있다면 2번 함수 호출, 다시 2번으로 루프
이렇게 돌아갈 것이다.
그리고 편의를 위한 함수로 유클리디안 거리를 계산하는 함수가 있으면 편할 것이고, 특정한 한 점과 centroid사이에서 최소의 centroid를 구하는 함수도 따로 분리하면 편할 것이다.
- 필요한 include
#include <vector>//vector
#include <math.h> //sqrt(for euclidean distance) 꼭 필요한 것은 아님..
그래서 구현한 소스가 아래와 같다..
// centroid를 리턴하는 함수
int KMeansClustering::GetCentroids(std::vector<std::vector<float>>& centroids)
{
centroids = this->m_vecCentroids;
return 0;
}
int KMeansClustering::GetCentroids(std::vector<std::vector<float>>& centroids)
{
centroids = this->m_vecCentroids;
return 0;
}
// k means 클러스터링을 실행한다.
int KMeansClustering::DoKMeansClustering(int kMeans , std::vector<int>& cluster)
{
//랜덤하게 centroid들을 초기화
for(unsigned int loop = 0 ; loop < this->m_vecData.size() ; loop++)
{
//cluster를 랜덤하게 배치해서 centroid를 지정하도록 한다.
this->m_vecCluster[loop] = rand() % kMeans;
}
int KMeansClustering::DoKMeansClustering(int kMeans , std::vector<int>& cluster)
{
//랜덤하게 centroid들을 초기화
for(unsigned int loop = 0 ; loop < this->m_vecData.size() ; loop++)
{
//cluster를 랜덤하게 배치해서 centroid를 지정하도록 한다.
this->m_vecCluster[loop] = rand() % kMeans;
}
int nModifiedNodes = 0;
do
{
this->CalculateCentroids();
this->SetMinimumDistances(nModifiedNodes);
do
{
this->CalculateCentroids();
this->SetMinimumDistances(nModifiedNodes);
}while(nModifiedNodes > 0);
return 0;
}
return 0;
}
// 최소 거리를 설정한다(파라미터 리턴 : 수정된 노드의 수)
int KMeansClustering::SetMinimumDistances(int& modifiedNodes)
{
int nModifiedNodeCount = 0;
int nClosestCentroid = 0;
int KMeansClustering::SetMinimumDistances(int& modifiedNodes)
{
int nModifiedNodeCount = 0;
int nClosestCentroid = 0;
for(unsigned int loop = 0 ; loop < this->m_vecData.size() ; loop++)
{
this->GetClosestCentroid(this->m_vecData[loop] , nClosestCentroid);
if(this->m_vecCluster.at(loop) != nClosestCentroid)
{
this->m_vecCluster.at(loop) = nClosestCentroid;
nModifiedNodeCount++;
}
}
{
this->GetClosestCentroid(this->m_vecData[loop] , nClosestCentroid);
if(this->m_vecCluster.at(loop) != nClosestCentroid)
{
this->m_vecCluster.at(loop) = nClosestCentroid;
nModifiedNodeCount++;
}
}
modifiedNodes = nModifiedNodeCount;
return 0;
}
}
// Centroids들을 계산해서 저장하는 함수
int KMeansClustering::CalculateCentroids(void)
{
std::vector<std::vector<float>> vecTotalPoints; //모든 포인트들의 총합 - k개 만큼의 데이터
std::vector<int> vecPointCount; //각 클러스터에 있는 점의 카운트
int KMeansClustering::CalculateCentroids(void)
{
std::vector<std::vector<float>> vecTotalPoints; //모든 포인트들의 총합 - k개 만큼의 데이터
std::vector<int> vecPointCount; //각 클러스터에 있는 점의 카운트
//총합, 평균을 구하기 위해 0으로 초기화
for(int loop = 0 ; loop < this->m_nK ; loop++)
{
std::vector<float> totVector;
for(int loopVec = 0 ; loopVec < this->m_nVectorSize ; loopVec++)
totVector.push_back(0);
vecTotalPoints.push_back(totVector);
vecPointCount.push_back(0);
}
vecPointCount.push_back(0);
}
//총합과 각 클러스터에 들어있는 점의 수를 구한다.
for(unsigned int loop = 0 ; loop < this->m_vecData.size() ; loop++)
{
for(int loopVec = 0 ; loopVec < this->m_nVectorSize ; loopVec++)
{
int nCluster = this->m_vecCluster.at(loop);
vecTotalPoints[nCluster][loopVec] += this->m_vecData[loop][loopVec];
vecPointCount[nCluster]++;
}
}
//Centroid에 평균점을 넣는다.
for(int loop = 0 ; loop < this->m_nK ; loop++)
{
for(int loopVec = 0 ; loopVec < this->m_nVectorSize ; loopVec++)
{
this->m_vecCentroids[loop][loopVec] = vecTotalPoints[loop][loopVec] / (float)vecPointCount[loop];
}
}
return 0;
}
// 데이터를 설정하는 함수
int KMeansClustering::SetData(std::vector<std::vector<float>> data)
{
this->m_vecData = data;
return 0;
}
int KMeansClustering::SetData(std::vector<std::vector<float>> data)
{
this->m_vecData = data;
return 0;
}
int KMeansClustering::SetData(float** data, int dataSize, int vectorSize)
{
this->m_vecData.clear();
{
this->m_vecData.clear();
for(int loopRow = 0 ; loopRow < dataSize ; loopRow++)
{
std::vector<float> inputData;
for(int loopCol = 0 ;loopCol < vectorSize ; loopCol++)
{
inputData.push_back(data[dataSize][vectorSize]);
}
this->m_vecData.push_back(inputData);
}
return 0;
}
{
std::vector<float> inputData;
for(int loopCol = 0 ;loopCol < vectorSize ; loopCol++)
{
inputData.push_back(data[dataSize][vectorSize]);
}
this->m_vecData.push_back(inputData);
}
return 0;
}
// 한 점에서 최소의 centroid를 구하는 함수
int KMeansClustering::GetClosestCentroid(std::vector<float> point, int& closestCentroidIndex)
{
float fMinDistance = -1;
float fDistance = 0;
int nMinCentroid = -1;
int KMeansClustering::GetClosestCentroid(std::vector<float> point, int& closestCentroidIndex)
{
float fMinDistance = -1;
float fDistance = 0;
int nMinCentroid = -1;
for(unsigned int loop = 0 ; loop < this->m_vecCentroids.size() ; loop++)
{
this->GetEuclideanDistance(this->m_vecCentroids.at(loop) , point , fDistance);
{
this->GetEuclideanDistance(this->m_vecCentroids.at(loop) , point , fDistance);
if(nMinCentroid == -1 || fDistance < fMinDistance)
{
fMinDistance = fDistance;
nMinCentroid = loop;
}
}
{
fMinDistance = fDistance;
nMinCentroid = loop;
}
}
closestCentroidIndex = nMinCentroid;
return 0;
}
}
// 유클리디안 거리를 구하는 함수
int KMeansClustering::GetEuclideanDistance(std::vector<float> x, std::vector<float> y, float& distance)
{
float fTotalSquareError = 0;
for(unsigned int loopx = 0 ; loopx < x.size() && loopx < y.size() ; loopx++)
{
fTotalSquareError += (x[loopx] - y[loopx]) * (x[loopx] - y[loopx]);
}
distance = sqrtf(fTotalSquareError);
return 0;
}
int KMeansClustering::GetEuclideanDistance(std::vector<float> x, std::vector<float> y, float& distance)
{
float fTotalSquareError = 0;
for(unsigned int loopx = 0 ; loopx < x.size() && loopx < y.size() ; loopx++)
{
fTotalSquareError += (x[loopx] - y[loopx]) * (x[loopx] - y[loopx]);
}
distance = sqrtf(fTotalSquareError);
return 0;
}
// float*의 오버로딩
int KMeansClustering::GetCluster(std::vector<float> data , int& clusterNum)
{
return this->GetClosestCentroid(data , clusterNum);
}
int KMeansClustering::GetCluster(std::vector<float> data , int& clusterNum)
{
return this->GetClosestCentroid(data , clusterNum);
}
int KMeansClustering::GetCluster(float* data, int dataSize , int& clusterNum)
{
std::vector<float> vecData;
for(int loop = 0 ; loop < dataSize ; loop++)
{
vecData.push_back(data[loop]);
}
{
std::vector<float> vecData;
for(int loop = 0 ; loop < dataSize ; loop++)
{
vecData.push_back(data[loop]);
}
return this->GetClosestCentroid(vecData , clusterNum);
}
}
// 파일에서 데이터를 로드해서 클러스터링을 한다
int KMeansClustering::LoadDataFromFile(const char* filename)
{
/*
* 파일포맷
*
* int : vectorSize;
* float float .... (vectorSize 만큼)
* float float .... (vectorSize 만큼)
* ...
*/
std::ifstream inputFile(filename);
int KMeansClustering::LoadDataFromFile(const char* filename)
{
/*
* 파일포맷
*
* int : vectorSize;
* float float .... (vectorSize 만큼)
* float float .... (vectorSize 만큼)
* ...
*/
std::ifstream inputFile(filename);
int vectorSize = 0;
inputFile >> vectorSize;
while(inputFile.eof())
{
float inputData;
std::vector<float> vecData;
{
float inputData;
std::vector<float> vecData;
for(int loop = 0 ; loop < vectorSize && inputFile.eof() ; loop++)
{
inputFile >> inputData;
vecData.push_back(inputData);
}
this->m_vecData.push_back(vecData);
}
{
inputFile >> inputData;
vecData.push_back(inputData);
}
this->m_vecData.push_back(vecData);
}
return 0;
}
}
뭐, 소스의 설명은 필요없을 정도로 직관적이다...
단지 변수들을 주의할 필요가 있을 것이다.
각 vec 변수들에 대하여 갯수와 용도를 잘 구분해서 파악해야할 것이다.
뭐, 이거는 테스트 없이 그냥 스크래치로 쭉~ 짠거라 잘 돌아갈지는 아직 모른다-_-;;
테스트를 위해 파일에서 로드하는 것도 했고,
그럼 파일로 테스트를 해보자.. 코딩하고 한번에 잘 되면 오히려 뭔가 찝찝하고 이상하다.. 파일로 테스트 하면서 몇 가지 초기화를 해야하는 문제라던가 루프를 돌 때 vector의 크기 문제 등을 간단하게 고치고 나면..
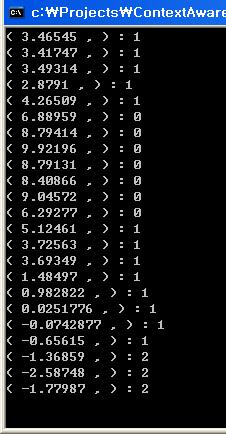
3단계로 나눴는데 얼추 되는것 같다..
클러스터0은 5이상인거 같고, 2는 -1 이하인것 같다..
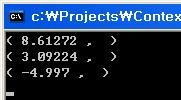
한번 클러스터의 평균점을 출력해보도록 했다. 두 클러스터의 중간 지점이 경계가 될 것이니 위에서 얼추 예상한 경계값과 맞는다. 아래는 k=5로 할 경우의 평균점 결과..
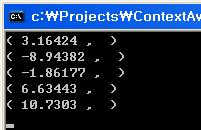
여기서 주의할 점을 발견했다! 순서가 저절로 소팅이 되는 것이 아니라 자기 멋대로 움직인다는 것! 나중에 클러스터링 후 처리로 소팅도 넣어주면 될 것이다. 근데 k=3에서 k=5로 바꾸니까 시간이 너무 오래 걸린다...-_- 고작 7319개 샘플 데이터 뿐인데...흑.. 차마 k=7을 돌려보기가 무섭다;; 최적화는 초기 상태의 선택이 얼마나 효과적으로 되었는지에 따라 달라질 것이다.. 그거에 대한 고민은 생략!
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- lecture
- ny-school
- mini project
- Javascript
- java
- 강좌
- TIP
- 안드로이드 앱 개발 기초
- google app engine
- HTML5 튜토리얼
- Python
- gae
- 탐론 17-50
- php
- HTML5
- 삼식이
- 안드로이드
- 샷
- 팁
- c++
- Writing
- gre
- 속깊은 자바스크립트 강좌
- 서울
- 사진
- Android
- 뽐뿌
- 자바스크립트
- GX-10
- K100D
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
