티스토리 뷰
K-means algorithm
K means 알고리즘에 대해서 이야기는 많이 들어왔는데, 그 돌아가는 방법에 대해서 알아보면 좋을 것 같다...
참고 자료는 위키피디아...
http://en.wikipedia.org/wiki/K-means_algorithm
- K-means algorithm은 k 파티션으로 클러스터링을 하는 것으로 expectation-maximization 알고리즘과 비슷하다고 한다. 왜냐하면 둘다 데이터의 안에 있는 중심을 찾으려고 하기 때문이라고 한다. Object attribute들이 벡터 공간을 형성한다고 가정하고 있고, 그 목적이 클러스터 내의 분산의 총합을 최소화하는 것이라고 한다.
squared error function V 는 다음 식과 같은데, k 클러스터로 나누는 것이고, S_i는 해당 클러스터, i = 1 ~ k, μ_i는 x_j∈S_i인 모든 값들에 대하여 centroid 또는 평균점이다.
// 여기까지는 뭐, 뻔한 내용.. k 개의 클러스터링을 목표로 하는 점.. 벡터 공간을 형성한다는 점, squared error 구하는 식이 보면 알겠지만, 각 클러스터의 데이터의 표준편차의 제곱, 즉 분산을 전부 합한 값이다. 쉬운 내용.. centroid와 평균점은 내용이 조금 다른데, centroid는 특정한 점이고, 평균 점은 특저한 점이 아닐 수 있다는게 다른 점이다.(아마도-_-;)
- 가장 잘 알려진 알고리즘의 형태는 iterative refinement heuristic으로 알려진 Lloyd's 알고리즘이다. 로이드의 알고리즘은 k개의 초기 상태로 나누는데, 초기에 랜덤으로 나누거나, 어떠한 heuristic한 데이터를 이용한다. 그래서 각 집합의 평균점이나 centroid를 계산한다. 그것은 각 지점을 가장 가까운 centroid에 할당함으로써 새로운 파티션이 생기게 되고, centroid들은 다시 새로운 클러스터를 위해서 계산되고, 알고리즘은 이 두가지 단계를 더 이상 점들이 클러스터를 바꾸게 되지 않을 때까지 계속적으로 반복한다.
//랜덤하게 나눈 set에 대해 중심점을 구하고 가장 가까운 노드들을 할당하는 것, 문제가 있다면 두 개의 centroid가 우연하게 같을 경우일 것 같다. 그 외에는 centroid는 점점 특정한 중심지점을 향해서 다가갈 것이다.
- Lloyd의 알고리즘과 k-means는 동일하게 사용되기도 하지만, Lloyd의 알고리즘은 사실적으로도 k-means 방법의 heuristic한 방법이기도 하다. 하지만 특정한 시작 지점과 centroid의 조합으로 인해 가끔씩 틀린 답으로 가는 경우가 발생한다(위의 최소화 함수의 optimal 답과 다른 경우로..)
//바로 위에서 말한 것과 같은 로이드 알고리즘이 문제가 있을 수 있다고 한다..
- 다른 방법도 존재한다. 로이드 알고리즘은 여전히 유용한 점이 접근을 매우 빨리 할 수 있다는 점이다. 사실, 검사하는 횟수가 점의 수보다 훨씬 적다는 것도 사실이다. 어쨋든, 최근에는 David Arthur and Sergei Vassilvitskii가 coreset에 대한 활용을 제안했다(coreset : 원래 데이터의 작은 subset)
- 성능에 대하여 알고리즘은 최적의 optimum을 보장하지는 못한다. 마지막 답은 초반의 클러스터링 셋에 많이 의존되며, 이 초기셋은 global optimum에 비해 많이 성능이 떨어져도 된다. 이 알고리즘이 매우 빠르므로, 일반적으로 이 알고리즘을 몇번 호출하고 찾아낸 최적의 클러스터링을 리턴하는 것이 일반적이다.
- 다른 주된 단점은 찾아야하는 클러스터의 수를 미리 정해줘야한다. 만약 데이터가 자연적으로 클러스터링 되어있지 않다면 이상한 결과를 얻을 수 있다. 또한, 알고리즘은 구면의 클러스터가 데이터에서 가능해야 잘 작동한다.
Demonstration of the algorithm
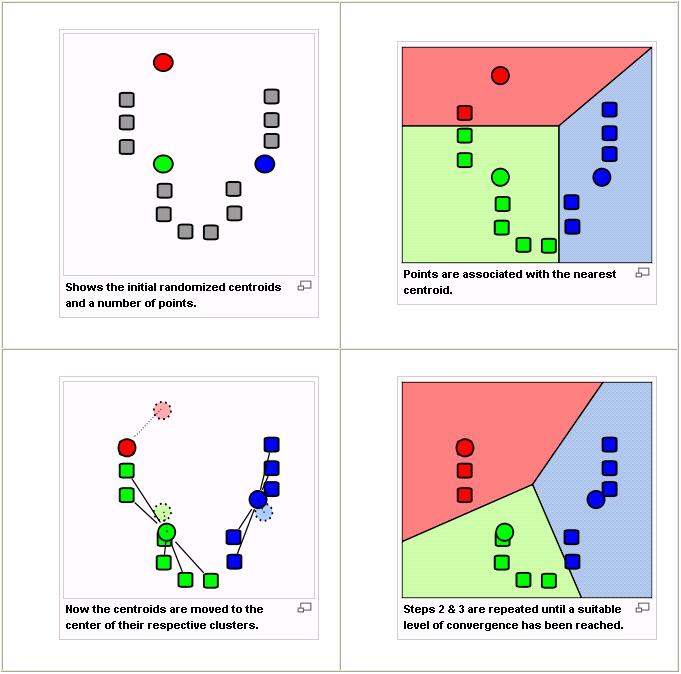
//방법만 봐도 대충 이해가 될 것이다. 아주 쉽다. k-means라고 하는 이유도 알 수 있고, 구현도 centroid를 구하는 함수, 각 최소 지점에 associate하는 함수(변환 여부를 bool로 리턴)만 있으면 될 것이다.
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- 사진
- mini project
- K100D
- 탐론 17-50
- Python
- HTML5
- 강좌
- 삼식이
- Android
- gre
- TIP
- c++
- 뽐뿌
- gae
- Javascript
- 서울
- 안드로이드
- HTML5 튜토리얼
- Writing
- 자바스크립트
- php
- 안드로이드 앱 개발 기초
- 속깊은 자바스크립트 강좌
- lecture
- google app engine
- GX-10
- 샷
- java
- ny-school
- 팁
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
