티스토리 뷰
Ch3. Single-Layer perceptron
2/27
3.1 Introduction
- NN이 형성되는 1943~1958에서는, 3명의 연구자들이 있었다. (1) McCulloch and Pitts(1943)은 NN을 computing machine으로 소개를 했다.
- (2) Hebb(1949)은 1st rule for self-organized learning을 가정했다.
- (3) Rosenblatt(1948)는 Perceptron을 learning with a teacher의 첫번째 모델로 제안했다.
3/27
- Perceptron은 NN의 가장 간단한 형태이다. linearly separable 패턴을 분류하는데 쓰인다.
- 이것은 single neuron과 adjustable synaptic weights와 bias로 이루어져있다.
- Perceptron convergence theorem은 perceptron이 분류할 수 있는 모든 것을 배울 수 있다는 것을 말하고 있다.
4/27
- Single neuron은 adaptive filter의 기본을 형성하고, 이는 Widrow와 Hoff(1960)에 의해 Least-mean-square algorithm으로 발전한다.
5/27
3.2 Adaptive filtering problem
- dynamical system에서 모든 입출력 데이터는 label되어있고 일정한 시간 단위로 저장되어있다.
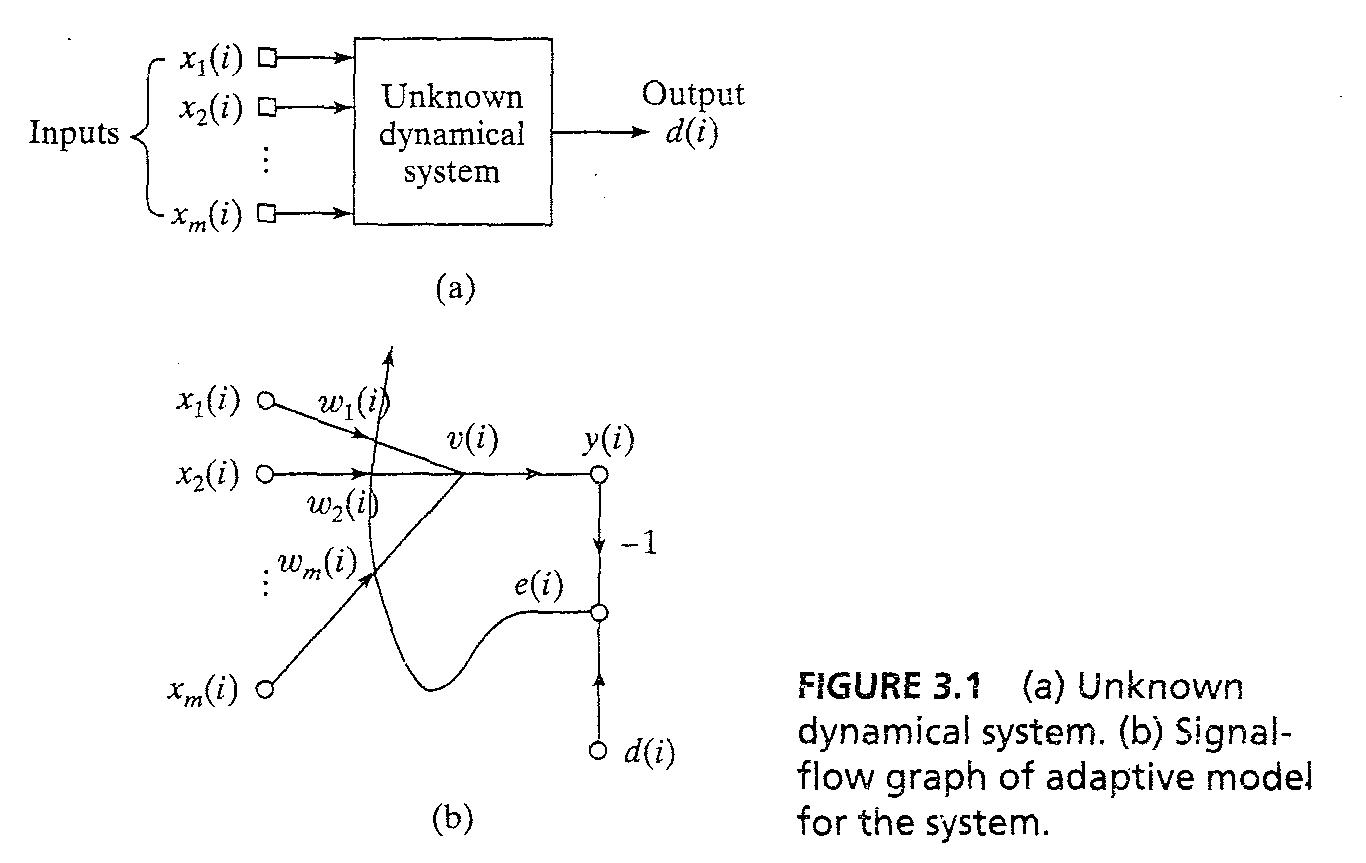
- System은 출력 d(i)를 Fig3.1과 같이 생산한다.
- 시스템의 external behavior는 다음 data set 에 의해 묘사된다. T:{x(i),d(i);i=1,2,3...}...3.1 where x(i) = {x_1(i), x_2(i), ... , x_m(i)}^T
- m 차원은 입력 공간의 차원수 또는 dimensionality이다.
7/27
- 자극 x(i)는 두개의 다른 방법으로 발생된다. sptial and temporal
- (1) m elements of x(i)는 공간에서 다른 점을 가리킨다, snapshot of data
- (2) m elements of x(i)는 현재와 m-1, 과거의 값들로 excitatino된 uniformly spaced in time을 나타낸다.
8/27
- 문제 : 알 수 없는 시스템의 multi input-single output 모델은 싱글 neuron으로 디자인
- neuronal model called adaptive filter는 synaptic weights를 adjustment하는 알고리즘으로 작동한다 : (1) 알고리즘은 arbitrary setting으로 시작한다; (2) adjustments는 연속적인 basis를 통해 만들어진다.; (3) 한 샘플링 period안에 computation is completed
9/27
- Fif 3.1b는 adaptive filter with two continuous operation인 signal-flow 그래프를 보여준다.
- (1) filtering process는 출력 신호 y(i)를 계산하고 에러 신호 e(i) = d(i) - y(i)이다
- (2) adaptive process는 자동으로 adjustment of synaptic weights with error signal e(i)
10/27
- Neuron은 linear이므로, 출력 y(i)는 Induced Local Field(ILF) v(i):y(i) = v(i) = sum(w_k(i)x_k(i)) ... 3.2
- matrix 형태로 y(i) = x^T(i)w(i) ... 3.3
- 일반적으로 y(i) <> d(i) 이고 e(i) = d(i) - y(i) ... 3.4
- 오류 신호은 weight를 adjust 하는 cost function에서 사용된다
11/27
3.5 LMS algorithm
- Least-Mean-Square는 instantaneous value를 기본으로 cost function을 위해 이용된다. 함수 ξ(w)= 1/2e^2(n) ... 3.33 where e(n)은 시간 n 때 계산된 error 신호이다
- differentiating ξ(w) with respect to weight vector w yields ðξ/ðw = e(n)*ðe(n)/ðw
12/27
- linear least-square filter와 같이 LMS 알고리즘은 linear neuron과 같이 operate한다. 따라서 우리는 에러 신호를 e(n) = d(n) - x^T(n)w(n) ... 3.35로 적고
- ðe(w)/ð(w(n) = -x(n)
- ðξ(w)/ðw(n) = -x(n)e(n)
- using this as estimate for gradient vector, g(n) = -x(n)e(n) ... 3.36
13/27
- 등식 3.36을 활용하여 등호 3.12에 넣으면 steepest descent, we formulate LMS algorithm as follows: w(n+1) = w(n) + ηx(n)e(n) ... 3.37
- η는 learning-rate parameter, weight vector w(n) 주위의 feedback loop는 low-pass filter처럼 작동한다.
- 등식 3.37에서 w(n)을 w(n)으로 바꿔서 LMS알고리즘은 estimate of weight vector를 생성한다는 것을 강조한다. where well-defined trajectory of steepest descent is sacrificed.
14/27
- LMS에서 w^(n)은 랜덤 궤도를 따라가고 LMS는 "stochastic gradient algorithm'으로 refer된다.
- iteration이 무한대로 가까워지면 w^(n) performs a random walk(Brownian motion) about Wiener solution w^0
- steepest descent와 달리, LMS알고리즘은 환경의 통계에 대한 knowledge를 요구하지 않는다.
15/27
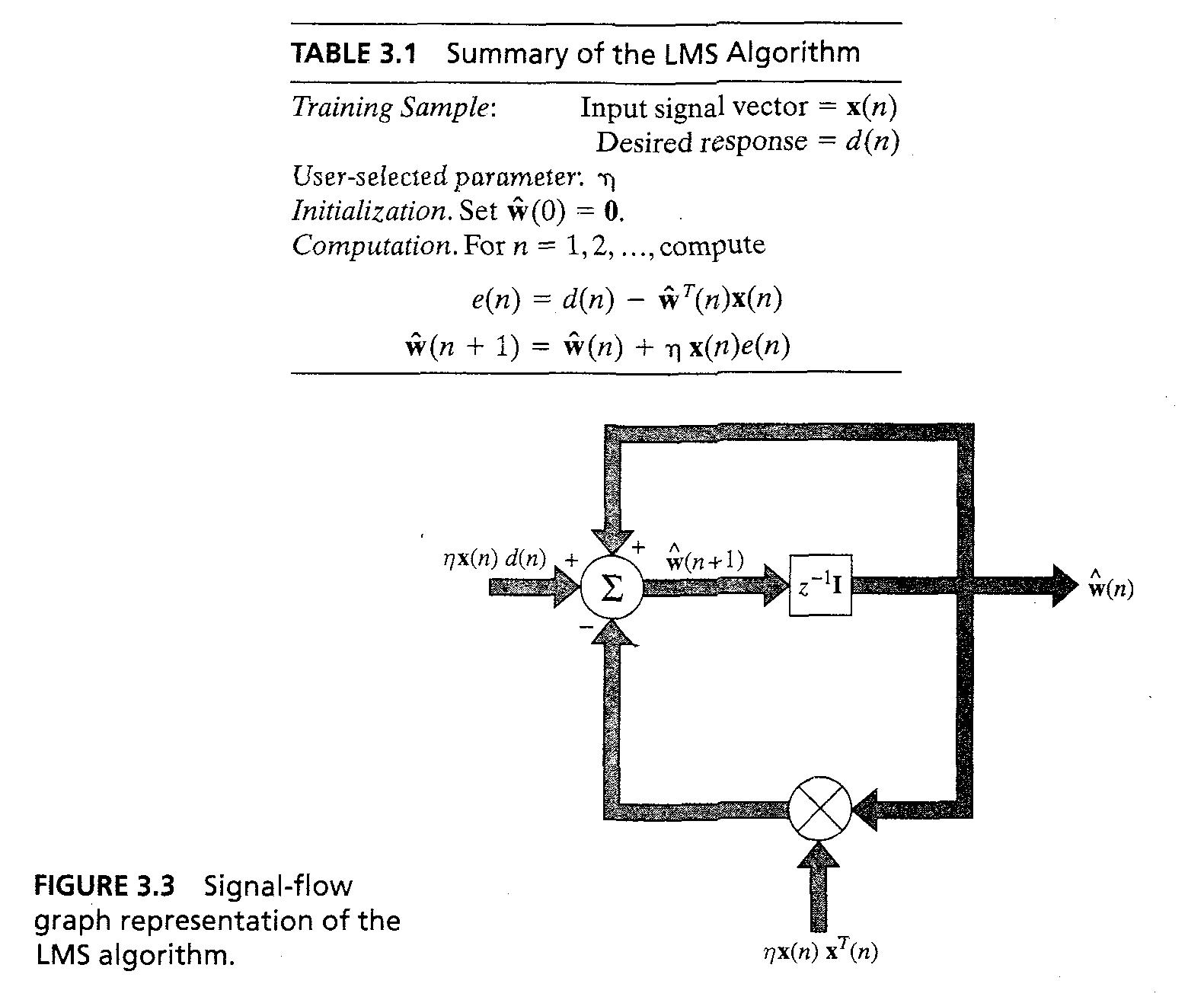
- LMS의 요약은 table 3.1에 있다. 일반적으로는 초기 데이터들을 0으로 설정한다.
- LMS 알고지름에서 우리는 w^(n) = z^-1[w^(n+1)] ... 3.39이다.
- LMS알고리즘의 Signal-flow graph는 Fig3.3에 있다. 이는 stochastic feedback system의 예를 보여준다.
17/27
3.8 Perceptron
- LMS 알고리즘은 built around linear neuron, 하지만 perceptron은 nonlinear neuron like McCulloch-Pitts model의 neuron의 주변에 있다.
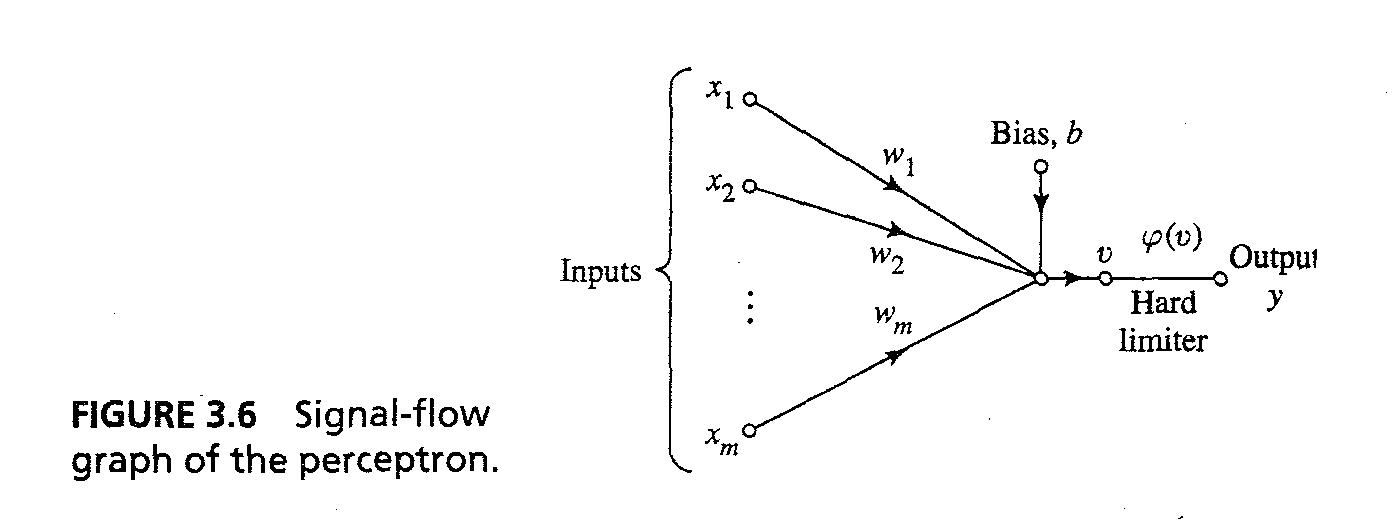
- Such neuron consist of linear combiner followed by hard limiter as signal-flow graph of Fig 3.6
- Induced Local Field or input to hard limiter is : v = sum(w_ix_i) + b ... 3.50 where b is external bias
3.9 Perceptron Convergence theorem
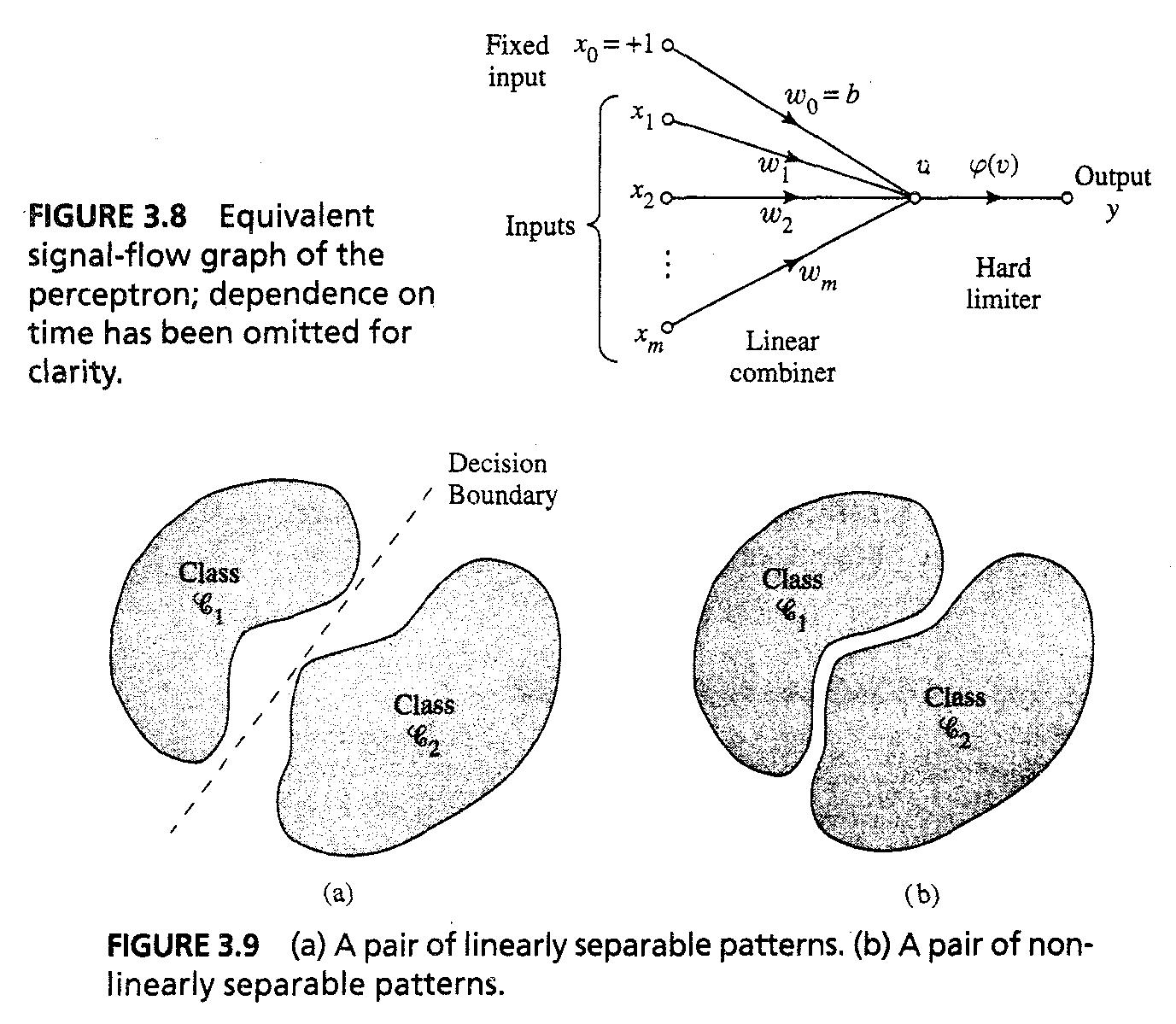
- Fig 3.8에서, bias b(n)은 synaptic weight로 여겨지고, linear combiner output는 다음과 같이 쓰인다 : v(n) = sum(w_i(n)x_i(n) = w^T(n)x(n)
- For fixed n, 등식 w^Tx = 0이 m-차원 공간에 plotted 될 경우 two differenct classe의 입력을 구분 짓는 hyperplane을 정의한다.
- For perceptron, 두개의 클래스 c1과 c2는 반드시 linearly separable해야한다
24/27
- Fig 3.9는 2-d perceptron의 예제를 보여준다.
- T1과 T2는 c1과 c2를 나타내는 training vector의 subset이고, union set of T!과 T2는 complete training set이다.
- Traning process는 adjustment of weight vector w so that c1과 c2가 linearly separable하도록 한다. x^Tx>0은 x∈C1과 w^Tx<=0은 x∈c2
25/27
- Perceptron의 weight vector 를 adapt하는 알고리즘
- (1) 만약 training set의 n번째 멤버가 x(n)이면, 이것은 weight vector w(n)으로 분류되고, 알고리즘의 n번째 interation에 계산된다. no correction is made:
- w(n+1) = w(n) if x^Tx(n)>0 and x(n)∈C1, w(n+1)=w(n) if w^Tx(n) <= 0 and x(n)∈c2
26/27
- (2) Otherwise, weight vector 는 다음 rule을 통해 update된다 : w(n+1) = w(n) - η(n)x(n) if w^Tx(n)>0 and x(n) ∈C1 where learning-rate parameter η(n)는 iteration n에서의 adjustment를 control 한다.
- When η(n) =η > 0, we have fixed increment adaptation rule.
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- ny-school
- K100D
- Python
- gae
- java
- 속깊은 자바스크립트 강좌
- lecture
- HTML5
- 탐론 17-50
- 자바스크립트
- TIP
- 강좌
- 팁
- gre
- Javascript
- GX-10
- Writing
- google app engine
- 샷
- HTML5 튜토리얼
- 안드로이드
- 사진
- 서울
- mini project
- Android
- php
- 뽐뿌
- 안드로이드 앱 개발 기초
- c++
- 삼식이
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
