티스토리 뷰
chap2a.ppt 자료를 바탕으로 정리...
2장의 제목은 Learning process.
지금 알고 있는 수준은 그냥 에러율을 계속 웨이트에 더해서 바꾸는것 정도...그럼 이제부터 시작..
2/38
2.1 Introduction
- 뉴럴네트워크(이하 NN)의 중요한 속성이 환경에서 'learn'하고 성능을 'improve'하는 것
- NN은 환경과의 상호작용을 통해서 그 synaptic weight와 bias를 조절하는 것이 learn이다.
- learn의 정의 : 환경의 자극요소들에 의해서 NN의 파라미터들이 적응되어가는 것. learning의 종류는 파라미터가 어떠한 방법으로 바꾸는지에 따라 정한다.
3/38
* 위의 정의는 다음을 의미한다. (1) NN은 환경에 의해 'stimulated'된다(2)NN은 free parameter로 자극의 결과에 의해 영향을 받는다. (3) NN은 내부의 변화 때문에 환경에 의해 'responds in new ways'함
- learning의 문제를 해결하는 미리 잘 정의된 룰의 집합을 "learning algorithm"이라고 한다.
- learning algorithem은 synaptic weight를 조절하는 방법에 따라 달리한다.
4/38
- 다른 요소는 NN이 어떻게 환경과 연관되느냐이다. "learning paradigm"은 NN과 작용하는 환경의 "model"에 영향을 받는다.
5/38
CH2. Learning Processes(Organization of Ch.)
- 2.2~2.6 은 5가지 기본 learning rules
- 2.7~2.9는 learning paradigm
- 2.10~2.12는 learning tasks, memory and adaptation을 실험한다.
- 2.13~2.15는 probabilistic과 statistical 관점의 learning을 다룸
6/38
2.2 Error-correction learning
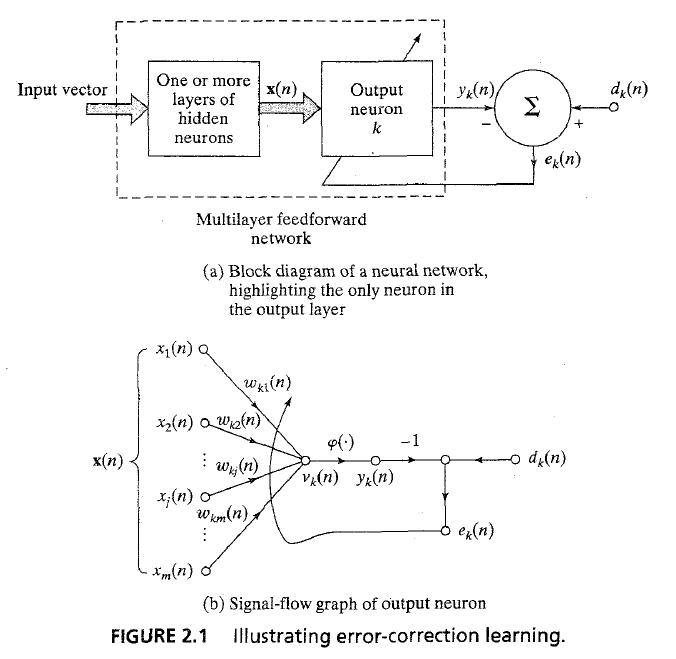
- feedforward NN의 단일 뉴런 k의 output layer가 Figure 2.1a. signal vector = x_n, n = discrete time, output signal = y_k(n)
- output signal은 'desired response' 또는 'target output' d_k(n)과 비교해서 'error signal' e_k(n)을 생성한다.
- e_k(n) = d_k(n) - y_k(n) ... (2.1)
8/38
- error signal e_k(n)은 'control mechanism'을 작동 시킨다. : 'control mechanism'는 뉴런 k의 synaptic weight를 알맞게 수정하는 과정.
- adjustment는 output signal y_k(n)을 derised response d_k(n)에 점점 가깝게 만드는 과정이다.
* 이 목표는 'cost function' 또는 'index of performance'E(n)을 최소화하는 것이다. 이것은 E(n) = sum(1/2*e_k^2(n)) ... (2.2)
: 뭐 지금까지는 쉬운 내용. 에러율은 원하는 값 - 나온값(2.1) 이고 모든 값들의 제곱(-일 경우와 +일 경우가 있으니깐..)의 합이 최소화하는 것.
9/38
- E(n)은 instantaneous value of error energy'이다. 뉴런 k의 synaptic weight에 대한 step-by-step 조정이 'steady state'에 이를때까지 learning 이 된다.
- learning process를 'error-correction learning'이라고 한다. cost function E(n)의 최소화는 'delta rule' 이나 'Widrow-Hoof rule'로 변할 수 있다.
10/38
- w_kj(n)이 뉴런 k의 synaptic weight w_kj를 나타낸다. signal vector x(n)의 원소 x_j(n)에 의해 시간 n에 자극된 w_kj.
- delta rule에서 Δw_kj(n) = ηe_k(n)x_j(n) ... (2.3) , η는 'rate of learning', 'learning rate parameter'
11/38
* 말로 바꾸면 '시넵틱웨이트에 가해지는 조정은 error signal에 비례하고, 시냅스에 대한 input signal에 대해 비례한다'
- 여기서 우리는 error signal은 'directly measurable'하다고 가정한다. fig 2.1a참고
- error-correction learning 은 환경에 'local'하다
12/38
- weight는 w_kj(n+1) = w_kj(n) + Δw_kj(n) ... 2.4
- w_kj(n) = z^-1[w_kj(n+1)] ... 2.5 와 같다. z^-1은 'unit delay operator' , 'storage element'를 나타냄
* error correction learning은 'closed loop feed back system'이다. learning rate parameter η가 learning performance의 key role이다.
13/38
2.3 Memory-based learning
* 'memory-based learning'에서는 과거 정확하게 분류된 입출력 예들을 저장한다. {x_i, d_i)}_i, x_i는 입력 벡터, d_i는 원하는 결과, i = 1..N
- test 입력 벡터 x_test, 알고리즘은 x_test의 'local neighborhood' 데이터들을 활용해서 훈련하고 분석하는 것이다.
* 두 가지 주요한 요소가 있음 : (1) local neighborhood를 구하는데 사용한 규칙 (2) training 예제들을 학습시킨 규칙
14/38
- 'nearest neighborhood rule' 에서는 local neighborhood는 test 벡터의 옆에 있는 학습 예제들이다.
- x'_N ∈{x_1,x_2,...,x_N} ... (2.6)은 x_test의 nearset neighbor이다. min_i d(x_i , x_test) = d(x'_N,x_test) ... 2.7, where d(x_i, x_test)는 유클리디안 거리
- 최소거리를 가진 vector x'_N에 할당된 class는 x_test의 분류(classification)로 한다
15/38
* Cover와 Hart(1967)은 NN-rule을 패턴인식 기반으로 했다.(2가지 가정을 놓음) (1) 분류된 예제들(x_i , d_j)는 'independently and identically distributed(iid)' (2) 샘플 크기 N은 무한히 크다
- 이 2가지 가정을 통해, nearest neighbor의 분류 에러 확률은 bayes probability of error의 두배가 된다.
16/38
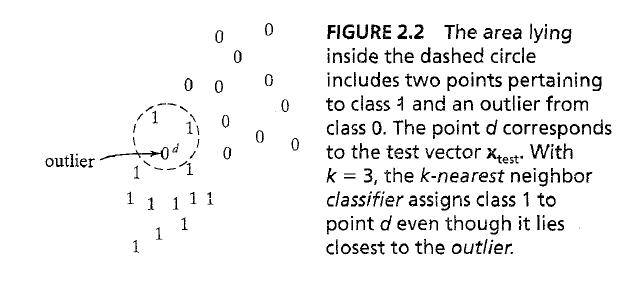
- nearest neighbor-rule의 한가지 k-NN 분류기 - (1) k개의 가장 가까운 패턴을 선택 (2) x_test를 k-NN중 가장 많은 것을 x_test에 선언
* k-NN은 평균 처럼 작용, outlier에 대해서 fig 2.2와 같이 대처한다(k=3)
18/38
2.4 Hebbian Learning
* Hebb's postulate learning은 가장 오래되고 가장 유명한 learning rule. 'the organization of behaviour(1949)' 부터 Hebb가 'when axon of cell A is near enough to excite cell B, and repeatedly takes part in firing it, some growth process or metabolic changes take place in one or both cells such that A's efficiency to fire B is increased'라고 했다.
- Hebb은 이 변화를 learning의 기본으로 삼았다.
19/38
* 확장하고 다시 말을 하자면, (1) 두개의 뉴런이 어느쪽의 시냅스이든 동시에 자극 받으면 시냅틱 웨이트는 증가한다; (2) 두 개의 뉴런이 비동기적으로 활성화되면 시냅스는 약해진다.
- 'Hebbian synapse'라고 불리우는 시냅스들은 'time-dependent, highly local, and strongly interactive mechanism to change synaptic efficiency as function of correlation between presynaptic and postsynaptic activities'
* 20/38
- Hebbian synapses의 4가지 속성(correlational synapse라고도 알려짐):
- 1. 'time- dependent mechanism' : 정확하게 일어난 시간에 의존적임
- 2. 'local mechanism' : spatiotemporal contiguity : 시공간적으로 근접
- 3. 'interactive mechanism' : 양쪽의 신호에 의존적임
- 4. 'conjunctional or correlational mechanism' : 동시에 일어나야함
21/38
2.4 Hebbian learning(Mathematical model)
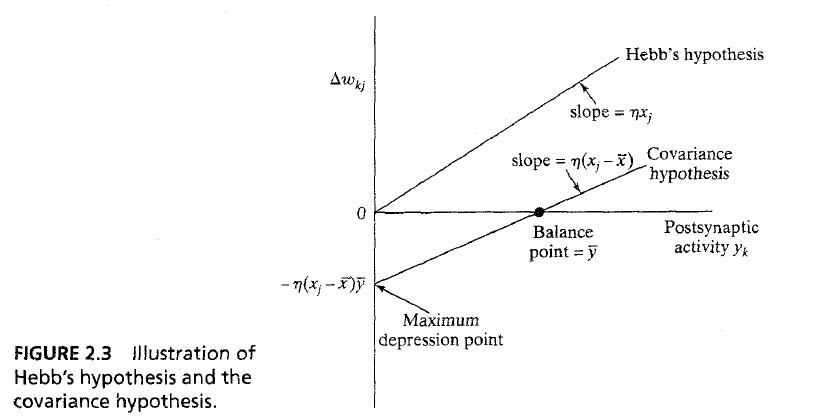
- Hebbian learning의 가장 간단한 형식은 : Δw_kj(n) = ηy_k(n)x_j(n) ... 2.9, where η는 rate of learning shown in top curve of fig 2.3
* 반복되는 행동은 exponential growth와 saturation을 일으킴
- Hebb 가설의 한계를 극복하기 위해 Sejnowski가 제안한 'covariance hypothesis'가 있다. signal을 평균으로 바꿔서 함
23/38
- Δw_kj=η(x_j-x)(y_k-y) ... 2.10 where x와 y는 'time-average values of presynaptic and postsynaptic'를 나타냄
- Fig 2.3은 그 다른 점을 보여줌
* covarience hypothesis allows (1) 평범한 상태로의 수렴을 안참(x_k=x, y_k=y) (2) potentiation과 depression에 대한 예측이 가능
24/38
2.5 Competitive learning
- 'Competitive learning'에서 NN의 출력 뉴런은 fired 되려고 경쟁함, 오직 한 가지 출력만이 한번에 active 됨
* 3개의 요소 (1) 같은 뉴런의 집합이지만 웨이트가 다르면 'responds differently' (2) 'limit'이 각 뉴런의 힘에 적용된다 (3) 'compete'의 메카니즘은 'winner-takes-all'의 방법을 사용한다.
25/38
- 개별적인 뉴런은 입력패턴의 feature detectors로 특징화 되어 다른 분류의 입력패턴을 분류한다
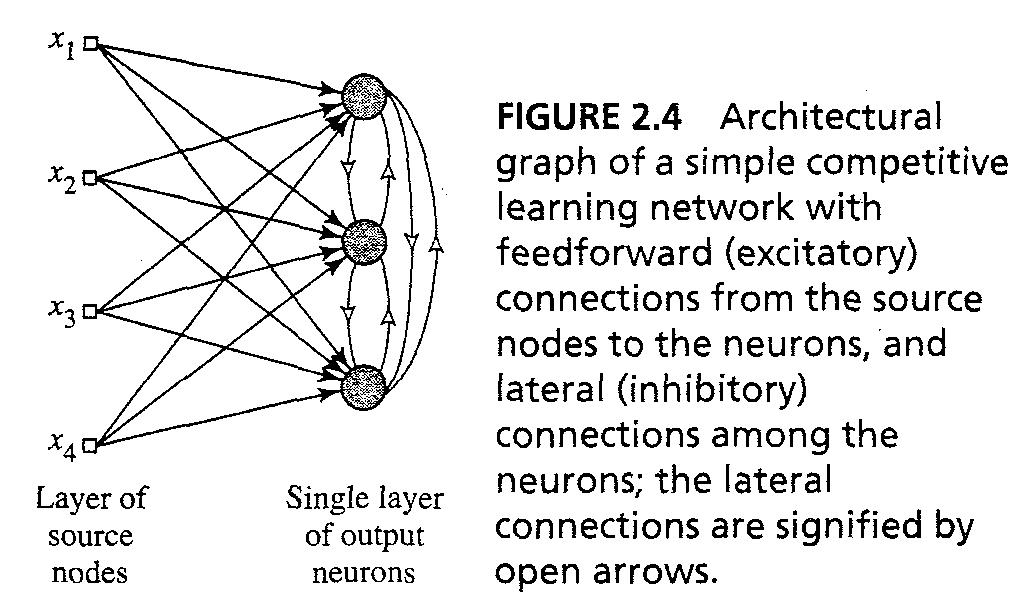
* 가장 간단한 예는 fig 2.4이다. feedback 연결이 lateral(근접) inhibition을 일으킴
- 뉴런 k가 활성화 되려면, 그것의 induced local field v_k가 입력 패턴 x에 대해서 가장 커야한다
27/38
* competitive learning rule은 다음과 같다 Δw_kj=η(x_j-w_kj) : k가 이겼으면, 졋으면 0 .. 2.13
- 이 rule은 이긴 뉴런 k의 웨이트 vector w_k를 입력 패턴 x에 다가가도록 한다
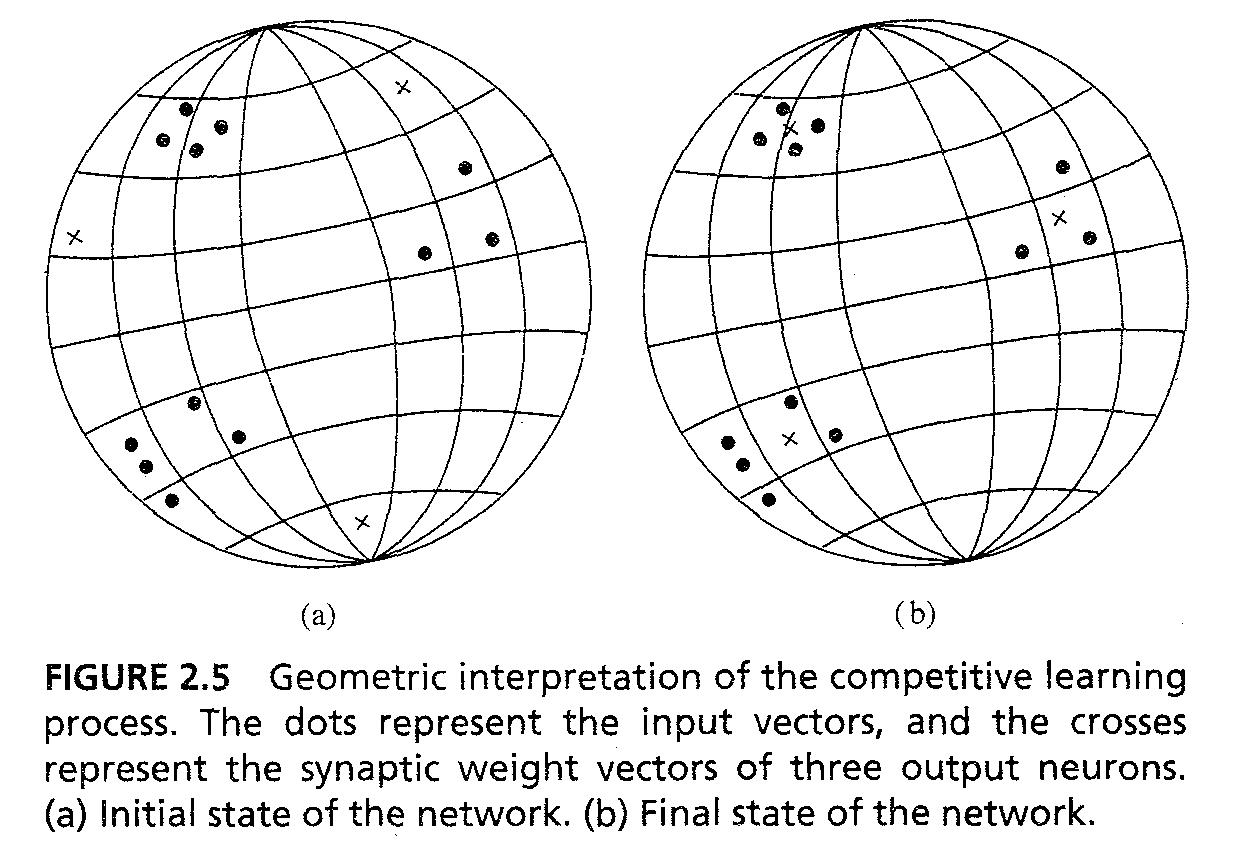
- Geometric analogy in fig 2.5는 핵심을 보여준다.
29/38
- 다음이 가정된다. (1) : 입력 패턴(벡터) x는 어떠한 일정 Euclidian 길이가 있다 (2) 모든 뉴런은 동일한 Euclidian 길이가 있다(norm) sum(w_kj^2) = 1 for all k ... 2.14
- Fig 2.5a는 초기 상태, Fig 2.5b는 특정한 마지막 상태, NN이 competitive learning을 통해서 clustering을 한 결과이다.
30/38
2.6 Boltzmann learning
- Boltzmann learning rule은 통계적 메카니즘에 기반한 확률적인 learning 알고리즘이다. boltzmann learning에 기반한 NN을 Boltzmann machine이라고 한다.
- Boltzmann machine의 뉴론은 순환되는 구조로, 바이너리모드로 진행된다. "on"일때는 +1, "off" 일때는 /-1. Boltzmann machine은 'energy function' E 의 특징이 있다. E=-1/2(sum_k,sum_j(w_kjx_kx_j)) ... 2.15 ,
31/38
- x_j 는 뉴런 j의 상태, w_kj의 뉴런j에서 뉴런k로의 시냅틱 웨이트, k<>j는 self-feedback이 없음을 뜻함
- machine은 뉴런을 랜덤으로 선택, 뉴런 k를 특정 온도 T에서 x_k에서 -x_k로 바꾼다. 확률은 P(x_k -> -x_k) = 1/(1+exp(-ΔE_k/T)) ... 2.16 where ΔE_k는 flip할 때 일어나는 energy change, T는 pseudotemperature
- 이 rule이 계속 적용되면 machine은 thermal equilibrium에 도달할 것이다.
32/38
- Boltzmann machine에 있는 뉴런은 2가지로 나뉜다 : 'visible' 과 'hidden', 'visible' 뉴런은 환경에 대한 인터페이스를 제공한다.
- 2가지 operation에 대한 모드가 있다 : 'clamped condition'은 visible 뉴런이 전부 고정된 상태에 고정되어있는 것, 'free-running condition은 모든 뉴런이 자유롭게 동작하는 것이다.
33/38
- Boltzmann learning룰에 의해 Δw_kj=η(ρ_kj^+ - ρ_kj^-) ... 2.17 where ρ_kj^+ 는 고정된 상태에서의 뉴런 j와 k의 correlation을 나타내고, ρ_kj^- 는 free running condition에서의 correlation이다. correlation은 -1~+1의 사이의 거리이다.
34/38
2.7 Credit-assignment problem
- Credit-assignment problem은 'credit'이나 'blame'이 learning machine에 따른 내부 결정에 따라 결정하게 된다. 이를 'loading problem'이라고도 부른다.
- 내부 결정에 의한 결과의 의존성은 learning machine의 동작 순서에 따라 바뀐다.
- credit-assignment problem은 두가지로 분류된다 (1) 결과에서 동작으로의 credit 설정은 temporal credit-assignment problem'이라고 선언된다. (2) 동작에서 내부 결정으로의 credit 설정은 structural credit-assignment problem이라고 한다.
35/38
- structural credit-assignment problem은 우리가 행동을 얼마나 바꿀지 선택해야하는 multi-component learning machine과 관련된다.
- Temporal CAP는 현재 시스템의 출력 결과로 가는 동작이 많을때, 어떠한 동작이 결과에 영향을 미치는지 정의하는 것과 관련된다.
- CAP는 multilayer feed forward NN일 경우 error-correction learning으로 나타낸다. 출력 뉴런들은 CAP는 쉽지만 hidden뉴런의 시냅틱 웨이트 조정에는 어렵다.
36/38
2.8 Learning with a teacher
- 학습 패러다임
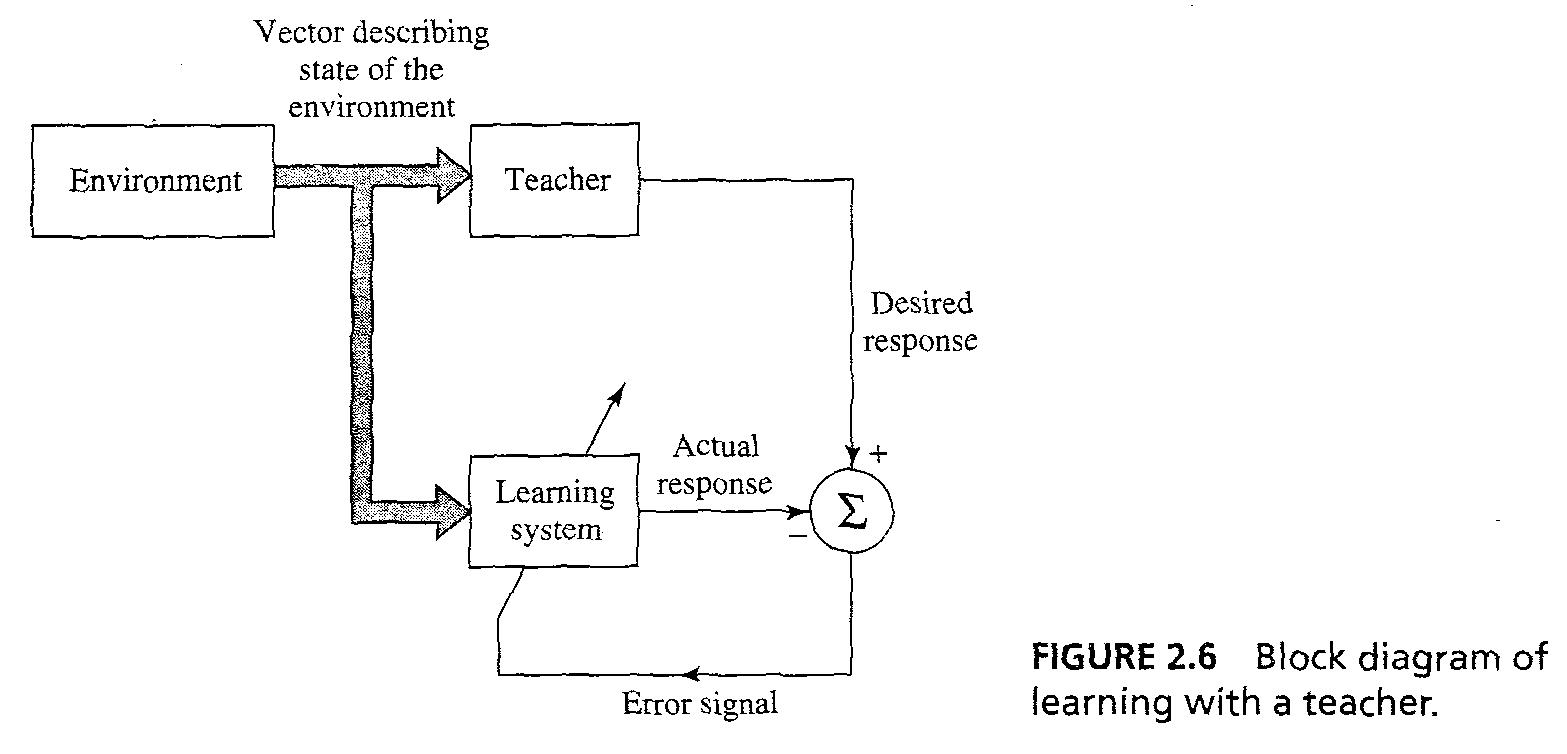
- 'Learning with a teacher' or 'supervised learning' in fig 2.6, teacher는 환경에 대한 지식이 있고 지식은 여러 개의 입출력 샘플을 나타낸다.
- NN 파라미터는 학습 벡터와 오류 신호로 조정된다.
- error signal은 desired response와 actual response사이의 차이이다.
- teacher와 비슷하게 되기 위해 step-by-step으로 반복적으로 조정이 가해진다.
38/38 (마지막! ㅠㅠ)
- 성능 계산 : mean-square error 나 squared error의 합을 학습 샘플을 통해서, free parameter NN의 함수로 정의 된다.
- 다차원에서 free parameter를 좌표로 한 error-performance surface나 error surface.
- 주어진 모든 operation은 error surface위의 한 점이고, performance를 개선하기 위해서 point를 아래쪽 최소로 이동 시켜야한다. 그것이 ;local'이든 'global'이든..
- 'gradient' of error surface에서의 한 점은 steepest descent 방향을 향하는 벡터이다.
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- ny-school
- c++
- gae
- google app engine
- 강좌
- Android
- mini project
- 속깊은 자바스크립트 강좌
- TIP
- 안드로이드
- 삼식이
- HTML5 튜토리얼
- java
- 탐론 17-50
- K100D
- Javascript
- 뽐뿌
- HTML5
- 서울
- gre
- 자바스크립트
- php
- Writing
- 팁
- 안드로이드 앱 개발 기초
- 샷
- Python
- lecture
- 사진
- GX-10
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
